論理関数の完全系とは、他の全ての論理関数をその関数の組み合わせだけで表現できる論理関数のセットを指します。例えばNAND、あるいはNORは組み合わせる事で、それだけで他の全ての論理関数を表現することができます。これは、NANDやNORが単独で完全系となることを意味します。

NORを用いたNOT回路
NOT回路は、入力の論理値を反転させる回路です。つまり、入力が0の場合は出力が1になり、入力が1の場合は出力が0になります。
NORゲートは、2つの入力のどちらも0の場合のみ出力が1となる論理ゲートです。それ以外の場合(すなわち、少なくとも1つの入力が1の場合)は出力が0になります。
NOT回路をNORゲートで表現するには、NORゲートの2つの入力に同じ値を供給します。このとき、NORゲートは次のように動作します:
- 入力が0の場合:
- NOR(0, 0) = 1 NORゲートの2つの入力が共に0の場合、出力は1になります。
- 入力が1の場合:
- NOR(1, 1) = 0 NORゲートの2つの入力が共に1の場合、出力は0になります。
このように、NORゲートの両方の入力に同じ値を供給することで、NOTの動作を模倣することができます。したがって、NORゲートを使用してNOT回路を実装することが可能です。
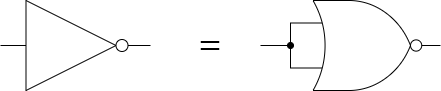
NANDを用いたNOT回路
NANDゲートは、2つの入力が共に1のときのみ出力が0となる論理ゲートです。それ以外の場合(すなわち、少なくとも1つの入力が0の場合)は出力が1になります。
NOT回路の動作をNANDゲートで再現するためには、NANDゲートの2つの入力端子に同じ信号を入力します。このとき、NANDゲートは以下のように動作します:
- 入力が0の場合:
- NAND(0, 0) = 1 NANDゲートの2つの入力が共に0の場合、出力は1になります。
- 入力が1の場合:
- NAND(1, 1) = 0 NANDゲートの2つの入力が共に1の場合、出力は0になります。
このように、NANDゲートの両方の入力に同じ値を供給することで、NOTの動作を模倣することができます。したがって、NANDゲートだけでNOT回路の動作を実現することが可能です。
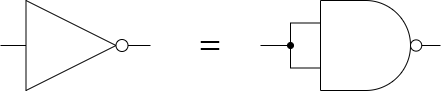
NOR(NAND)回路を用いたOR(AND)回路
先ほどのNOR(NAND)回路を使ったNOT回路を応用すると、NOR(NAND)だけでOR(AND)回路も構成できます。
手順は以下の通りです:
- AとBの2つの入力を最初のNOR(NAND)ゲートに入力します。この出力はA NOR(NAND) Bとなります。
- A NOR(NAND) Bの出力を次のNOR(NAND)ゲートの2つの入力に接続します。
- この2段階のNORゲートの出力は、A OR(AND) Bとなります。

NOR回路を用いたAND回路
NOR回路のみを用いてAND回路を構成することが出来ます。
- AのNOTを取得する
AのNOTは次のように表現できます。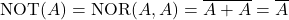
- BのNOTを取得する
同様に、BのNOTも次のように表現できます。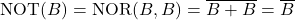
- AND動作の再現
2つのNOT出力を次のNORゲートに入力として供給します。
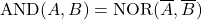
この式を変形します。ド・モルガンの法則を用いて、論理和の否定は論理積の否定の否定と等しいので、次の変形が行えます。
![]()
論理否定の論理否定は元の値と等しいので、
![]()
したがって、この最後のNORゲートの出力は、AとBのANDの結果、つまり![]() と等しくなります。
と等しくなります。
MIL記号であらわすと以下の通りです。
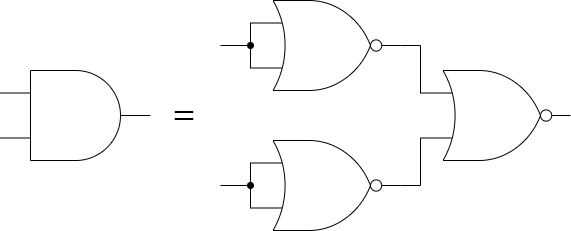
ORも同様にNANDのみを用いて構成することが出来ます。

等価変換のメリット
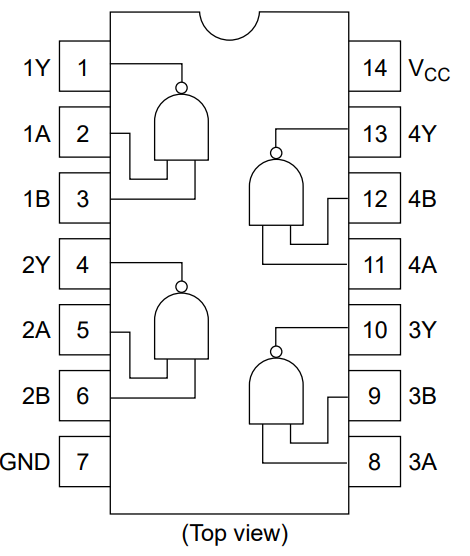
実際に回路を構成する際に製造の簡略化やコスト削減が期待できます。例えば一般的な論理ICは複数の論理ゲートがいつのICに組み込まれています。下記は74HC01という最も一般的な論理ICの外観とピンの配置図です。
1つのICに4つのNANDゲートが搭載されています。
この回路を用いてAND回路を構成する際に、等価変換を行わないと別のNOTゲートを用意する必要が有ります。等価変換を行えばこのIC1つでAND回路を構成する事が出来る為、製造コストが削減できます。

https://pdf1.alldatasheet.jp/datasheet-pdf/view/63804/HITACHI/74HC01.html
確認テスト
XORをNANDのみで表せ
▼ヒント(クリックして展開)
下記の式を変形してゆきます。
![]()
解答と解説は次のページへ
