論理関数は、主に「加法形 (Sum-of-Products, SOP)」と「乗法形 (Product-of-Sums, POS)」の2つの形式で表現されることがあります。これらの形式は、デジタル回路の設計を単純化するための手段として用いられます。

加法形 (Sum-of-Products, SOP)
加法形は、一つ以上の積項(AND演算による項)の和(OR演算)として表される論理式です。各項が複数の変数またはその否定の論理積(AND演算)であり、これらの積項が論理和(OR演算)で結ばれている状態を示します。
例えば、A、B、Cという変数を持つ関数があるとします。加法形の一つの例は以下のようになります。
![]()
これは、「A AND B」、「B AND C」、または「C AND A」のいずれかが真(1)であれば、関数Zは真(1)になるということを示しています。

乗法形 (Product-of-Sums, POS)
乗法形は、一つ以上の和項(OR演算による項)の積(AND演算)として表される論理式です。各項が複数の変数またはその否定の論理和(OR演算)であり、これらの和項が論理積(AND演算)で結ばれている状態の式を言います。
引き続きA、B、Cの変数を使用した関数を例に取ると、乗法形の一つの例は以下のようになります。
![]()
これは、「A OR B」、「B OR C」、および「C OR A」のすべてが真(1)である場合に限り、関数Zが真(1)になることを示しています。

加法標準形と乗法標準形
加法形、乗法形の論理関数において、各項がすべての論理変数を含んでいる場合、加法標準形または乗法標準形といいます。逆に加法標準形、乗法標準形を簡略化したものが加法形、乗法形となります。以下に各標準形の例を示します。
加法標準形:
![]()
この式の各項はすべての変数A,B,Cを含んでおり、この時の各項を最小項といいます。
与えられた関数を変換し、最小項の和で表現する手法を最小項和表示あるいは主加法標準展開といいます。
乗法標準形:
![]()
この式の各項はすべての変数A,B,Cを含んでおり、この時の各項を最大項といいます。
与えられた関数を変換し、最大項の積で表現する手法を最大項積表示あるいは主乗法標準展開といいます。
標準形と真理値表
標準形と真理値表は1対1に対応しており、片方が分かればもう片方は容易に導出する事が可能です。以下に3変数の場合の論理式と真理値表の対応を示します。

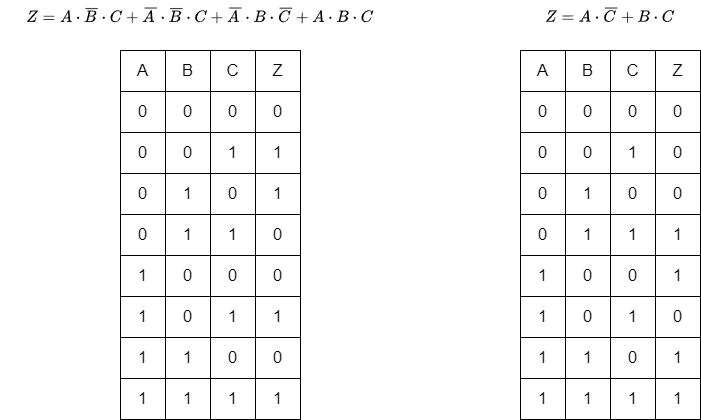
例:この対応から例えば以下の真理値表を示す場合には以下の数式を簡単に導くことが出来ます。
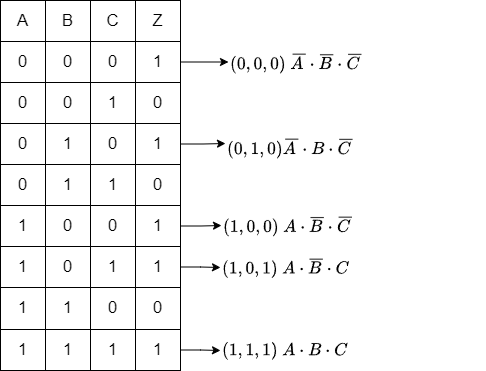
最小項の標準形(加法標準形):この式は、論理関数が '1' を出力する各場合の論理和です。各項は、その入力の組み合わせが関数の出力を '1' にすることを表しています。
![]()
最大項の標準形(乗法標準形):この式は、論理関数が '0' を出力する各場合の論理積です。各項は、その入力の組み合わせが関数の出力を '0' にすることを表しています。最大項の各項は論理和(OR)であり、これらの項全体の積が関数全体を形成します。
![]()
例題①
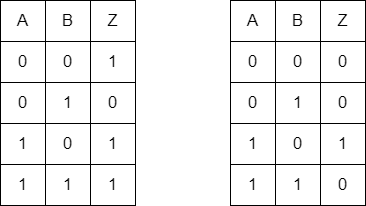
右に示す真理値表に対応する論理式(加法標準形)を求めてください。
解答はこちらをクリック
例題②
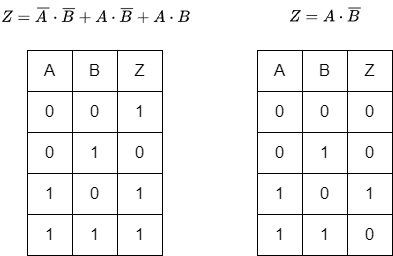
各論理式(加法標準形)に従い、真理値表の空欄を埋めてください。
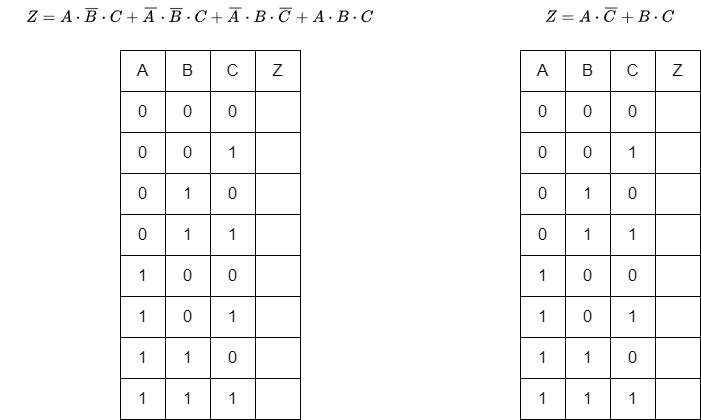
解答はこちらをクリック