論理回路は、デジタルシステムの基本的な構成要素であり、主に組み合わせ回路と順序回路の2つのタイプに分類されます。これらの回路は、コンピュータ、デジタル時計、電卓など、私たちの日常生活の多くのデバイスにおいて中心的な役割を果たしています。
組み合わせ回路は、その名が示す通り、複数の論理ゲートを組み合わせて構成されます。このタイプの回路は、入力の現在の状態のみに基づいて出力を決定します。つまり、過去の入力や回路の前の状態は出力に影響を与えません。これは、組み合わせ回路が「メモリレス」であるということを意味します。
一方、順序回路は、現在の入力とともに過去の状態(つまり「記憶」)を考慮に入れて出力を決定します。これにより、順序回路は時間とともにその状態を変化させることができ、より複雑なタスクを実行する能力を持ちます。
本テキストでは、組み合わせ回路に焦点を当て、その動作原理、構造、そして応用例について詳しく掘り下げていきます。組み合わせ回路の理解を深めることで、デジタルシステムの設計と分析における基礎的な知識が得られるでしょう。

論理回路図の書き方
組合せ回路では多くのMIL記号を組み合わせて論理回路図を書きます。その際、あえて記号を置き換えて記載する事で論理回路を直観的に分かりやすくする場合があります。
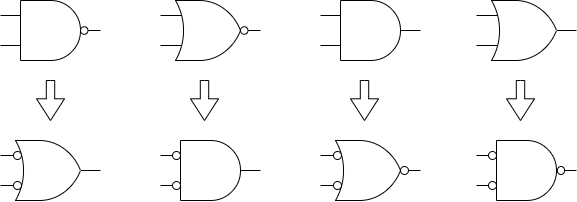
例えば以下の通りNANDゲートのみで以下の回路を構成する場合、入力に対する出力値の関係が直観的には分かり辛いです。同様の働きをする回路でも左の図の様に示した場合はそれぞれの入力をANDした結果をORしている事が直観的に理解することが出来ます。
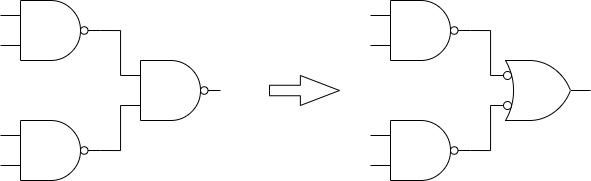
NAND構成への変換
NANDゲートは【論理関数③】完全系で述べた通りそれだけで他の全ての論理関数を表現することができます。加法形の論理関数はAND項のOR接続なので、簡単に変換することが出来ます。例えば以下の式をMIL記号で表すと以下の通りです。

ここでNANDゲートへの置き換えを考えてみます。ANDゲートはNANDゲートの出力をNOTゲートに置き換えたものとして考えることが出来ます。ORゲートはNANDゲートの入力にNOTゲートを加えたものと考えることが出来ます。
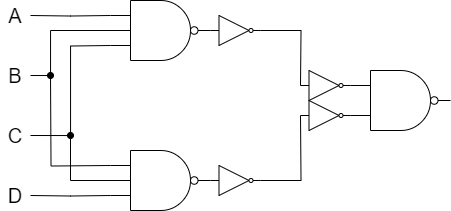
2段のNOTゲートは消すことが出来ますので最終的には以下のようになります。
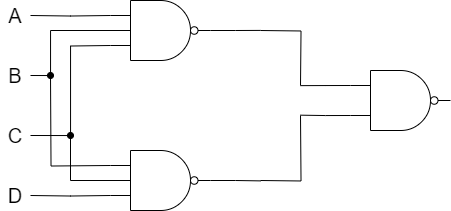
半加算器
半加算器(Harf Adder:HA)は、デジタル回路設計において基本的な構成要素の一つで、二つの1ビットの数値(通常は二進数の数値)を加算する機能を持ちます。半加算器は、足し算の結果として得られる「和(Sum)」と、その際に生じる可能性のある「桁上げ(Carry)」の2つの出力を生成します。前の段からの桁上がりの考慮はありません。
入出力
半加算器の入出力の関係は以下のようになります。
- 入力 A = 0, B = 0 の場合: 和 S = 0, 桁上げ C = 0
- 入力 A = 0, B = 1 の場合: 和 S = 1, 桁上げ C = 0
- 入力 A = 1, B = 0 の場合: 和 S = 1, 桁上げ C = 0
- 入力 A = 1, B = 1 の場合: 和 S = 0, 桁上げ C = 1
この最後のケースでは、和が0で桁上げが1となり、これは二進数での加算において「10」となります(つまり2を表す)。
真理値表は以下の通りです。
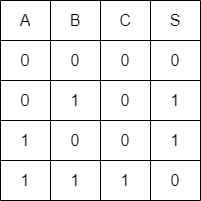
半加算器の構成
上記の真理値表から半加算器を設計してみます。加法標準系を求めるとSの値は下記の通りとなり、下記の論理回路が構成できます。

XORにまとめる事もできる為,半加算器は、最終的に主に以下の2つの基本論理ゲートから構成されます。回路図は以下の通りです。省略して右の図のように示されることもあります。
- XORゲート(排他的論理和): 2つの入力が異なる場合に1を出力し、同じ場合には0を出力します。これにより、加算の際の「和」が計算されます。
- ANDゲート: 2つの入力が両方とも1の場合にのみ1を出力し、それ以外の場合には0を出力します。これにより、桁上げ(Carry)が発生するかどうかを判定します。
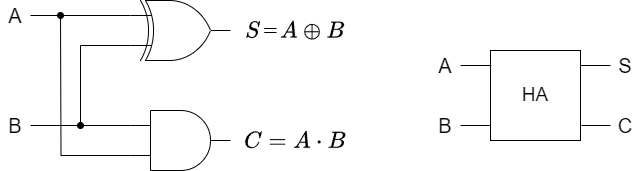
全加算器
全加算器(Full Adder:FA)は、デジタル回路の基本要素で、3つの1ビット入力(2つの加算対象ビットと1つの桁上げ入力)を加算する機能を持ちます。フル加算器の主な目的は、2ビットの加算において前の桁からの桁上げを含めることです。これにより、より大規模な加算器を構築して、複数ビットの数値の加算が可能になります。
入出力
全加算器は、以下の要素から構成されます。
- 入力: 2つの加算対象ビット(AとB)と、前の桁からの桁上げ入力(Carry-In、Cinと表記されることが多い)。
- 出力: 加算結果の和(Sum、S)と、次の桁への桁上げ出力(Carry-Out、Cout)。
真理値表は以下の通りです。
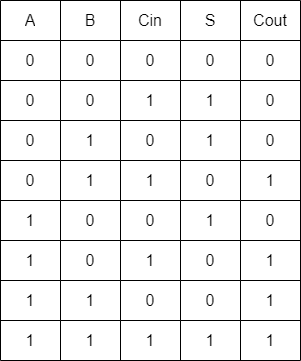
全加算器の構成
上記の真理値表から全加算回路を設計してみます。
今までで練習してきたように、まずは真理値表から加法標準系を求め,そこからXORが出現するように式を変形してゆきます。
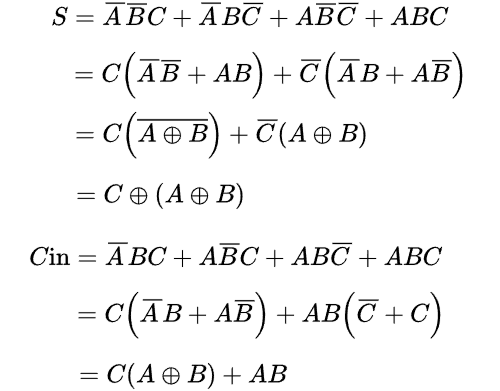
これを論理回路図にすると以下の通りになります。

さらに、半加算回路が2個で構成されていることが分かりますので,下の図の様に示されることもあります。
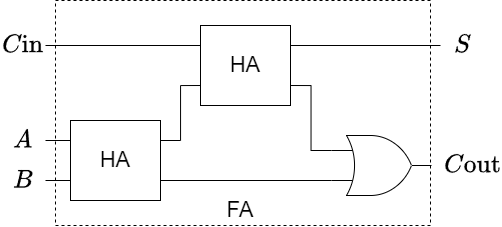
- 和(Sum): 3つの入力(A, B, Cin)のXORゲートを用いた組み合わせによって計算されます。具体的には、AとBのXORゲートの出力とCinのXORゲートの出力を再度XORします。
- 桁上げ出力(Carry-Out): 3つの入力のうち少なくとも2つが1の場合に1になります。これは通常、複数のANDゲートとORゲートを組み合わせて計算されます。
