前回は2進の加算器を設計しました。
この回路と補数の考え方を使う事で、減算器を作ることが出来ます。
全加算器を使った補数加算の回路は、2進数の減算を加算として行うために使用されます。補数加算法は、引き算を直接行う代わりに、特定の数(被減数)から引かれる数(減数)の補数を加算することで減算を実現します。

2進減算器の概要
補数の概念
- 補数: ある数を特定の基数(例: 10や2)まで足したときの差。
- 2進数における補数:
- 1の補数: すべてのビットを反転(0は1に、1は0に)することで求められます。
- 2の補数: 1の補数に1を加えることで求められます。2進数での減算に一般的に使われます。
補数を使った減算のプロセス
- 減数の2の補数を求める: 減数の全ビットを反転させ、その結果に1を加えます。
- 全加算器で加算する: 得られた2の補数を被減数に加算します。
- 結果の解釈:
- オーバーフロー: 加算結果がオーバーフロー(桁あふれ)した場合、最上位ビットを無視します。
- 正の結果: オーバーフローしない場合、結果はそのまま正の値として受け取ります。
- 負の結果: オーバーフローした場合、結果は負であり、その2の補数を取ることで実際の値を得ます。
全加算器の役割
- ビットごとの加算: 全加算器は各ビットの加算を行い、桁上がりを次のビットの加算に反映します。
- 連続した加算: 複数ビットの数を加算する際に、全加算器は連続して配置されます。
実用例
この方法はコンピュータやデジタル機器で一般的に使用され、特にCPU内の算術論理ユニット(ALU)で重要な役割を果たします。ALUは加算、減算、および他の論理演算を行う部分で、補数加算の原理は効率的な減算を可能にします。
補数器の設計
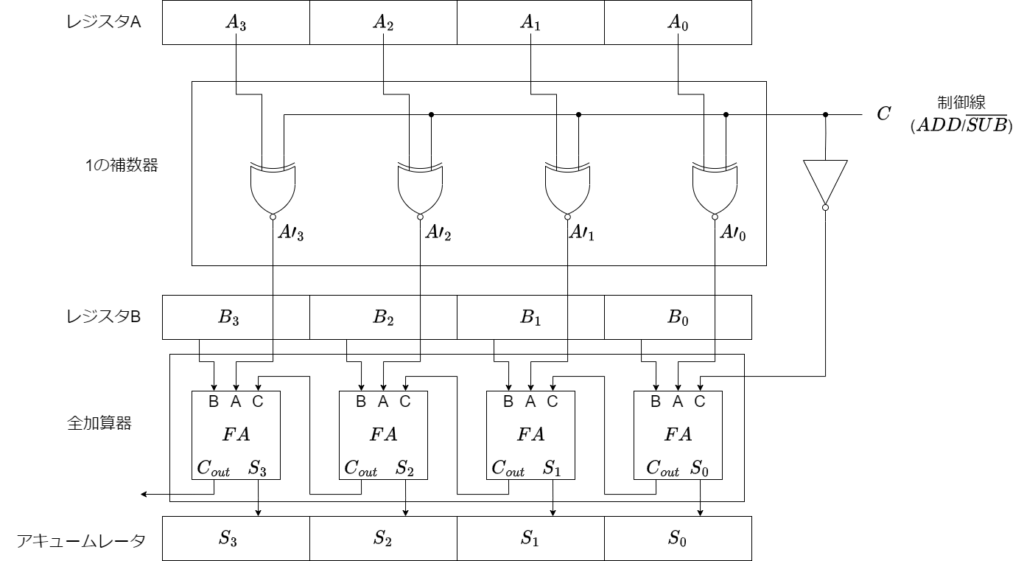
今回は4ビットの加算、減算を行える装置を設計してゆきます。
足し算をする場合はそのままの出力をし、引き算をする場合は入力を反転し、1足す回路を作らなくてはいけません。
足し算か引き算かを判断する信号をCとします。Cが1の時(ADD)足し算され、Cが0の時(SUB)引き算されます。
すると以下のような真理値表が得られます。
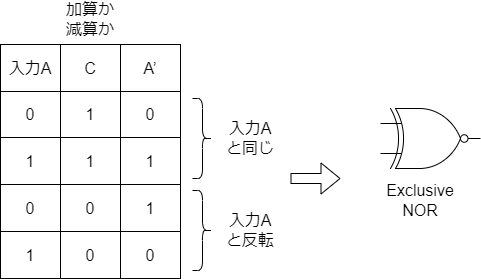
真理値表を観察するとXNORになっていることがわかります。
よって4ビットの1の補数器は以下のようになります。

加減算器の動作原理
加減算器は、加算モードと減算モードの両方を実行できるように設計されています。
- 加算モード:
- 全加算器は通常通り加算を行います。
- 入力された2つの数はそのまま加算器に供給され、和が出力されます。
- 減算モード:
- 減算を行うために、まず減数を1の補数器を通して反転させます。
- 反転させた減数と被減数(引かれる数)を全加算器に供給します。
- この時、全加算器の最初の桁上がり(Cin)には「1」を入力します。これは、1の補数を使う減算では、2の補数を生成するために必要です。
- 全加算器は反転された減数と被減数に1を加えた結果(実質的には2の補数減算)を出力します。
この考え方を前回設計した4ビットの加算器に適応することで4ビットの加減算器を設計することが出来ます。
回路図は以下の通りです。