論理関数とは
論理関数とは、論理値(真または偽)を入力として受け取り、論理値を出力する関数のことを指します。論理関数は、論理回路やプログラムなどの分野でよく使われます。
論理回路では1がHIGHレベル(例えば5V),0がLowレベル(例えば0V)に対応します。
論理関数 Z は0または1の値をもち、以下のような式で表されます。
![]()
ここで、
- B はブール値の集合 {0, 1} です。
- n は論理関数が受け取る論理変数の数です。
- f は論理関数自体を指します。
2つの論理変数 A と B に対するAND関数は以下のように表現されます。(ANDについては後程詳しく解説します)
![]()

真理値表
真理値表(または真理表)は、論理式や論理関数の動作を表すための表です。この表は、全ての可能な入力の組み合わせに対する出力の値を示しています。ブール代数やデジタルロジック設計のコンテキストで使用されることが多いです。
真理値表は、通常、行と列で構成されます。
- 行: 入力の全ての可能な組み合わせを示す。2つの論理変数がある場合、4つの行が存在する(22=422=4)。3つの論理変数の場合、8つの行が存在する(23=823=8)というように、論理変数の数に応じて行数が増える。
- 列: 論理変数とその論理変数の組み合わせに対する出力を示す。最後の列は該当する論理関数または論理式の出力を示す。
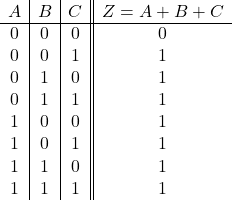
次に下記の図の通り、3つのスイッチが接続されている回路について真理値表を考えてみましょう。
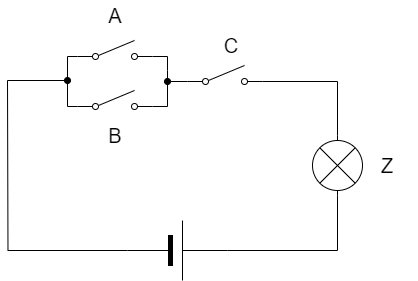
スイッチそれぞれを論理変数 A, B, および C とすると、その全ての可能な状態の組み合わせは![]() 通り存在します。
通り存在します。
ここでは、スイッチの状態を以下のように定義します。
- オン: 1 (真)
- オフ: 0 (偽)
次に、どのようなロジック(論理関数)がこの回路に適用されるかを考える必要があります。
スイッチAとBが並列に接続されている場合、スイッチAまたはスイッチBのいずれかがオンになると、その後の部分に電流が流れます。
その後、スイッチCが直列に接続されているので、Cがオンでなければ電流は流れません。
この関係を出力結果をZとして真理値表に表すと以下の通りになります。
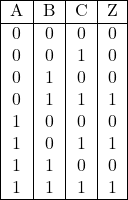
この表は真理値表といい、入力値のすべての組み合わせに対して関数がどのような出力を返すかを示しています。
基本的な論理関数
以下に7つの基本的な論理関数についてその論理式と真理値表、MIL記号、ベン図を示していきます。論理ゲートと呼ぶこともあります。
OR(論理和)
OR回路の出力は、少なくとも1つの入力が高い(通常は論理値「1」または高電圧)場合に高くなります。すべての入力が低い(通常は論理値「0」または低電圧)場合にのみ、出力は低くなります。
基本的な特性:
- すべての入力が「0」のときのみ、出力が「0」となります。
- いずれかの入力が「1」であれば、出力も「1」となります。
以下にMIL記号とベン図を示します。MIL記号(またはMIL標準記号、軍用標準記号)は、電気回路の構成要素を示すためのグラフィックシンボル群を指します。ベン図は、集合の関係を図示する方法として知られています。論理回路では入力信号の組み合わせとそれに対応する出力を視覚的に表現することができます。
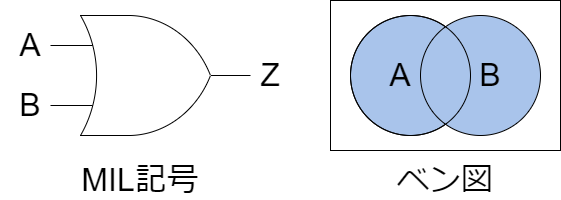
2入力の論理式:
![]()
2入力の真理値表:
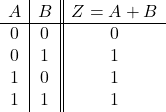
3入力の論理式:
![]()
3入力の真理値表:
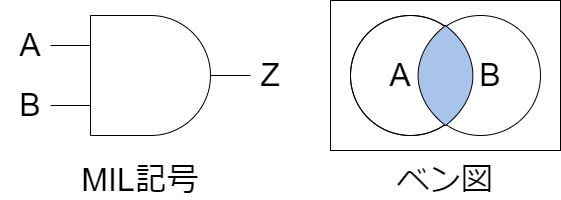
AND(論理積)
AND回路は、すべての入力が高い(通常は論理値「1」または高電圧)場合にのみ、出力を高くします。それ以外の場合、出力は低い(通常は論理値「0」または低電圧)です。
基本的な特性:
- 全ての入力が「1」のときのみ、出力が「1」となります。
- いずれかの入力が「0」であれば、出力も「0」となります。
以下にMIL記号とベン図を示します。
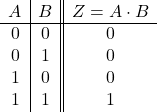
2入力の論理式:
![]()
2入力の真理値表:
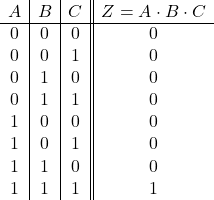
3入力の論理式:
![]()
3入力の真理値表:
NOT(否定)
NOT回路はデジタル論理の基本的なゲートの一つです。この回路は、入力の論理値を反転させる機能を持っています。つまり、入力が高い(通常は論理値「1」または高電圧)場合、出力は低く(論理値「0」または低電圧)なります。逆に、入力が低い場合、出力は高くなります。
基本的な特性:
- 入力が「1」のとき、出力は「0」となります。
- 入力が「0」のとき、出力は「1」となります。
以下にMIL記号とベン図を示します。
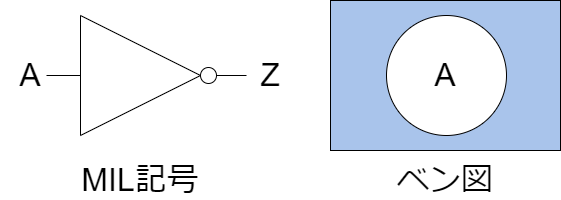
論理式
![]()
真理値表
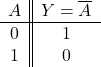
NOR(否定論理和)
NOR回路は、OR回路の出力を反転したものです。2つ以上の入力のいずれも高くない場合(すべて0の場合)にのみ、出力が高くなります。いずれかの入力が高い場合、出力は低くなります。
基本的な特性:
- すべての入力が「0」のときのみ、出力が「1」となります。
- いずれかの入力が「1」であれば、出力も「0」となります。
以下にMIL記号とベン図を示します。
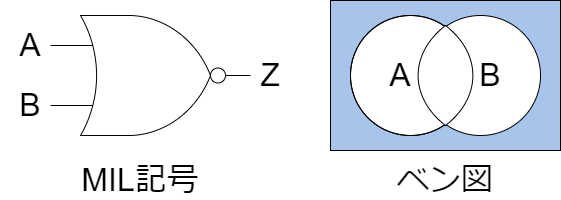
論理式
![]()
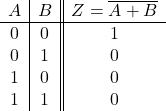
真理値表
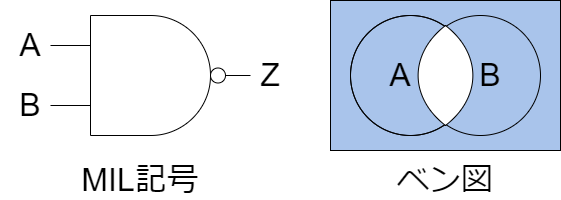
NAND(否定論理積)
NAND回路は、AND回路の出力を反転したものです。2つの入力の両方が高い場合(すなわち、1の場合)にのみ、出力が低くなります。その他の場合、出力は高くなります。
基本的な特性:
- すべての入力が「1」のときのみ、出力が「0」となります。
- いずれかの入力が「0」であれば、出力は「1」となります。
以下にMIL記号とベン図を示します。
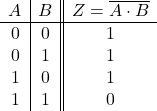
論理式
![]()
真理値表
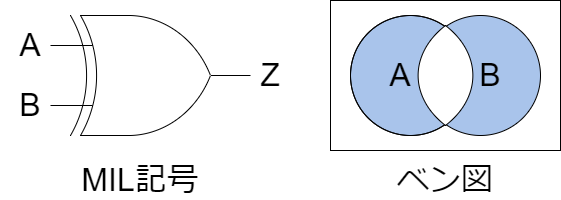
XOR(排他的論理和)
XORは「排他的論理和」とも呼ばれ、2つの入力のうち1つだけが「1」の場合に出力が「1」となる論理ゲートです。入力が同じ値(すなわち、0-0または1-1)の場合、出力は「0」となります。
基本的な特性:
- 入力が異なる場合(0-1または1-0)、出力は「1」です。
- 入力が同じ場合(0-0または1-1)、出力は「0」です。
以下にMIL記号とベン図を示します。
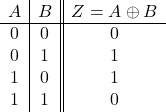
論理式
![]()
真理値表
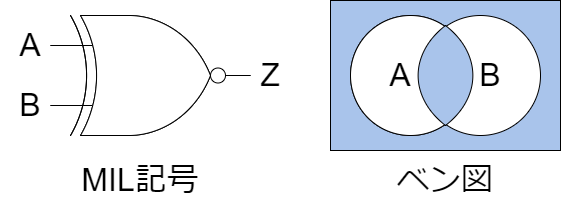
XNOR(一致)
XNORは、2つの入力が同じ場合にのみ出力が「1」となる論理ゲートです。もし2つの入力が異なる場合(すなわち、0-1または1-0)には、出力は「0」となります。XNORは、XORの出力を反転したものとしても考えることができます。
基本的な特性:
- 入力が同じ場合(0-0または1-1)、出力は「1」です。
- 入力が異なる場合(0-1または1-0)、出力は「0」です。
以下にMIL記号とベン図を示します。
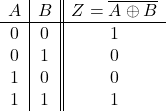
論理式
![]()
真理値表
確認テスト
論理関数①確認テストはこちら論理回路の作図
論理回路の作図は少しめんどくさいですが、下記にお勧めツールを紹介してますので、参考にして下さい。

