実際の論理回路の設計においては必ずしもすべての最小項が入力に使用されない場合があります。入力に使用しない項の出力結果を0と1どちらでも良いと定義することによってより論理回路の簡単化を行うことが出来ます。本日は冗長項について解説していきます。

冗長項とは
実際の論理回路の設計においては必ずしもすべての最小項が入力に使用されない場合があります。例えば電卓などのボタンから0~9の値を入力して、2進数に変換して計算を行う場合、(BCD (Binary-Coded Decimal) 符号化といいます)0から9までの各10進数が、それぞれの4ビット2進数コードに変換されます。真理値表は以下の通りになります。出力Zは入力された値が5以上だった場合に1が出力される回路と仮定しています。
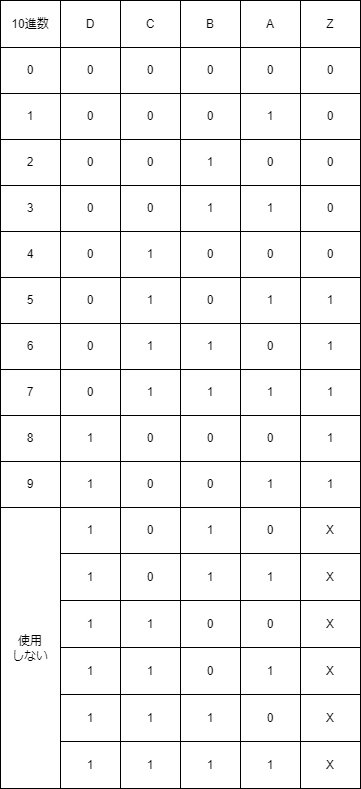
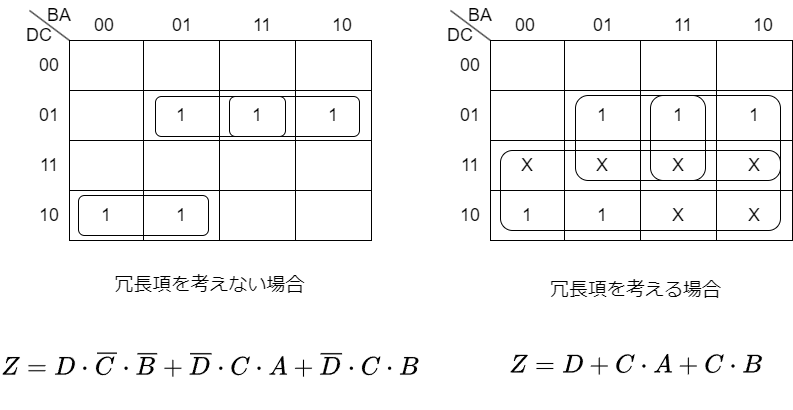
テンキーには0~9までのボタンしかありませんので、4桁の2進数で本来表現できる、10~15に対応する10進数は使用しないことになります。よってZの出力値は0でも1でも良いことになります。この状態でカルノー図を考えてみましょう。
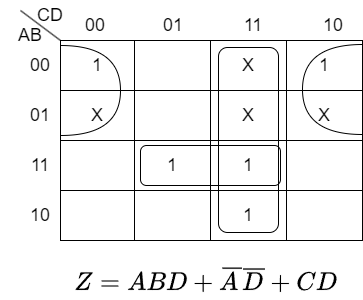
左のカルノー図は冗長項を考えない場合です。冗長項は0と1どちらをとっても良いので、右のカルノー図の様に、大きくグルーピングを行うことが出来ます。その結果下記の通り式の簡略化が行えました。
例題
(1)次の式をカルノー図を用いて簡略化せよ。
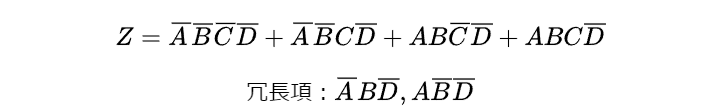
解答はこちらをクリック
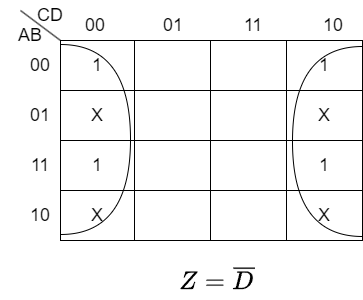
(2)次の式をカルノー図を用いて簡略化せよ。

解答はこちらをクリック