カルノー図(Karnaugh map、K-mapとも呼ばれます)は、デジタル回路設計において、特にブール代数の論理関数を簡略化するのに使われる図解的なツールです。この方法は、複雑な論理式を簡単にし、最小限の論理ゲートでの実装を可能にするために使用されます。これは、ハードウェアのコストを削減し、回路の効率と信頼性を向上させるのに役立ちます。

2変数のカルノー図
カルノー図(Karnaugh map、K-map)は最小項を2次元的に配置した図のことを指します。直観的な手順で最も単純な論理式を導くことが出来きます。しかし変数が多くなると2次元平面上での表現が難しくなりますので、主に4変数以下の場合に広く利用されます。
以下に2変数の場合のカルノー図を示します。縦列と横列はそれぞれ変数AとBに対応しており、それぞれが0か1を取ることになりますので4つの区画に区切られます。
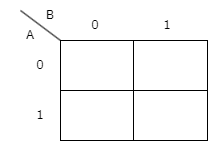
次に実際にカルノー図を使って式の簡略化をしていきます。手順は以下の通りです。
- 変数の識別とカルノー図の作成:関数のすべての入力変数を識別し、これらを用いてカルノー図を構築します。カルノー図のサイズ(セルの数)は、変数の数によって決まります(例:2変数なら4セル、3変数なら8セル)。
- 値のマッピング:論理関数から得られる出力値(真理値表から)をカルノー図にマッピングします。各セルには、特定の入力組み合わせに対する出力値が配置されます。
- グルーピング:「1」の値を持つ隣接するセルをグループ化します。これらのグループは、2の累乗のサイズ(2、4、8など)でなければなりません。グループは、必要なゲート数を最小限に抑えるために、できるだけ大きく作成します。その際表の上下では隣接している扱いになります。グループは重複していても構いません。
- 論理式の簡約:最後に、各グループから簡略化されたブール論理式を生成します。これは、グループ化されたセルに対応する変数の論理和を取ることによって行われます。
試しにカルノー図を使って![]() を簡略化してみましょう。
を簡略化してみましょう。
1.カルノー図の枠を作成します。
2.真理値表の出力列を埋める要領で、X=1 となるマスに「1」を記入します。0は記入しません。真理値表が与えられている場合は真理値表から転記します。今回は第1項の![]() が1になる場合と、第2項の
が1になる場合と、第2項の![]() が1となる場合に1を記入します。
が1となる場合に1を記入します。
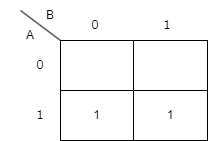
3.上下左右(≠斜め)で1が隣接する区画を、2^nマス単位の四角形で可能な限り大きく囲みます。(つまり、1、2、4、8マス単位の四角形でできるだけ大きく囲む)。なお、1が記入されたマスは1つ以上の囲みに属さなければならない(複数の囲みに属してもよい)。
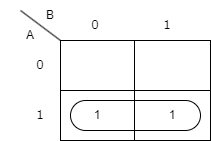
4.囲まれた区画に共通する成分を項とした論理和で論理式を構成します。これにより求められた論理式は最小積和形となります。
![]()
確認
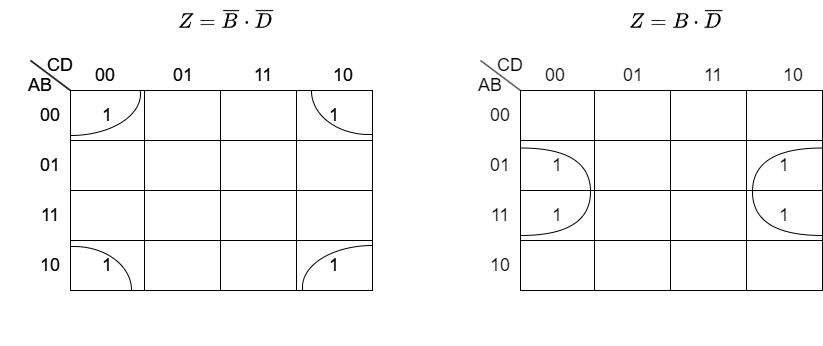
次のカルノー図から最小積和形の論理式を求めよ。
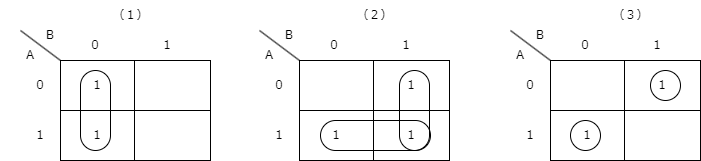
解答はこちらをクリック
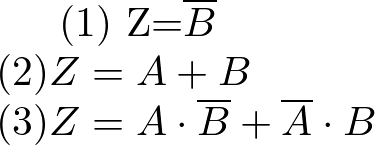
3変数のカルノー図
3変数のカルノー図の場合は以下の図を使います。
この際、 列は、上から順番に「00」→「01」→「11」→「10」のように数字がひとつだけ変化するように構成しなければなりません。(この規則を満たせば「10」→「11」→「01」→「00」でもかまわない) また、次に示すように、(見出しを除いた)最上列と最下列はつながっていると見なして、1のマスを囲む必要があります。
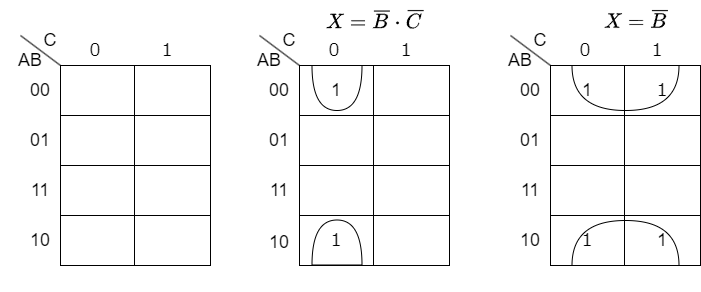
確認
次のカルノー図(完成済み)から論理式(最小積和形)を構成してください。
解答はこちらをクリック
4変数のカルノー図
4変数の場合、カルノー図は下のように作成する。この際、 列と 行は「00」→「01」→「11 」→「10」のように数字がひとつだけ変化するように構成しなければならない。また、3変数のカルノー図が上下に循環していたように、4変数の場合は、上下と左右に循環している。
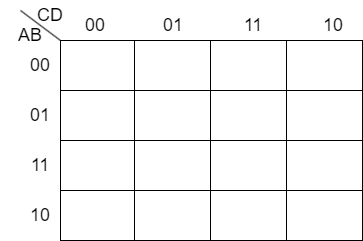
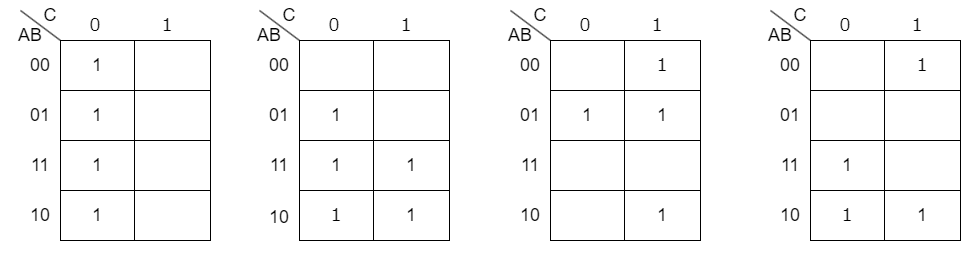
確認
次の4変数カルノー図から論理式(最小積和形)を構成してください。
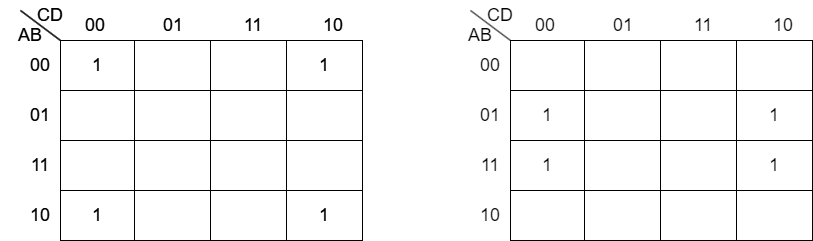
解答はこちらをクリック