デジタル回路 回路 論理関数 高専2年生

【論理関数②】ブール代数

ブール代数（または論理代数）は、論理計算の基礎となる数学の分野です。変数は2つの値しか取りません。これらの値は「0」と「1」として表され、または「真」と「偽」としても解釈されます。これを2値論理といいます。

この2値論理はド・モルガンやブールらによって論理代数としてまとめられ、ブール代数と呼ばれています。

ブール代数は、デジタル回路の設計やコンピュータの基礎となる技術に非常に重要な役割を果たしています。論理ゲート（AND、OR、NOTなどの基本的なデジタル回路）の動作原理や、より複雑な回路の動作を理解・設計するための基盤となっています。

ブール代数の基本法則

べき等則　(Idempotent Law)

べき等則は、ブール代数における基本的な法則の一つで、任意の変数Aに対して次の関係が成り立ちます。

これらの法則は、変数とその変数自体との論理和または論理積を取ると、元の変数の値がそのまま返されることを示しています。

  • 論理和のべき等則:

    $$ A + A = A $$

  • 論理積のべき等則:

    $$ A \cdot A = A $$

交換則　(Commutative Law)

交換則は、ブール代数の二項演算において、計算の順序を交換しても結果が変わらないことを示す法則です。具体的には、任意の変数AとBに対して次の関係が成り立ちます。

  • 論理和の交換則:

    $$ A + B = B + A $$

  • 論理積の交換則:

    $$ A \cdot B = B \cdot A $$

結合則　(Associative Law)

結合則は、ブール代数の三つの項に関する演算において、項のまとめ方を変えても結果が変わらないことを示す法則です。具体的には、任意の変数 A、B、および C に対して次の関係が成り立ちます。

  • 論理和の結合則:

    $$ A + (B + C) = (A + B) + C $$

  • 論理積の結合則:

    $$ A \cdot (B \cdot C) = (A \cdot B) \cdot C $$

分配則　(Distributive Law)

分配則は、ブール代数における複数の項に関する演算の関係性を示す法則で、一つの演算が別の二つの演算の間で分配できることを示しています。具体的には、任意の変数 A、B、および C に対して次の関係が成り立ちます。

  • 論理和と論理積の分配則:

    $$ A \cdot (B + C) = (A \cdot B) + (A \cdot C) $$

  • 論理積と論理和の分配則:

    $$ A + (B \cdot C) = (A + B) \cdot (A + C) $$

吸収則　(Absorption Law)

吸収則は、ブール代数の特定の構造を持つ項に関する演算の結果を示す法則です。この法則により、一部の情報が「吸収」されることで、式が簡略化されることを示します。具体的には、任意の変数 A と B に対して、次の関係が成り立ちます。

  • 論理和と論理積の吸収則:

    $$ A + (A \cdot B) = A $$

  • 論理積と論理和の吸収則:

    $$ A \cdot (A + B) = A $$

2重否定　(Double Negation)

2重否定は、ブール代数において変数を2回否定した場合、元の変数の値がそのまま返されるという性質を示す法則です。具体的には、任意の変数 A に対して、次の関係が成り立ちます。

    $$ \overline {\overline A} = A $$

補元則 　(Complement Laws)

補元則は、ブール代数における各論理変数とその否定（補数）との関係を示す法則です。具体的には、次の2つの法則から成り立っています。

論理和の相補性：変数とその否定を論理和した場合、常に真となることを示しています。

    $$ A + \overline A = 1 $$

論理積の相補性：変数とその否定を論理積した場合、常に偽となることを示しています。

    $$ A \cdot \overline A = 0 $$

恒等則 　(Identity Laws)

恒等則は、論理和や論理積を取る際に、特定の値を用いると元の値が変わらないことを示す法則です。具体的には以下の2つの法則から成り立っています。

  • 論理和の恒等則：ある論理値と0（偽）を論理和すると、その論理値は変わらない

    $$ A + 0 = A $$

  • 論理積の恒等則：ある論理値と1（真）を論理積すると、その論理値は変わらない。

    $$ A \cdot 1 = A $$

ド・モルガンの法則　(De Morgan's Laws)

ド・モルガンの法則はブール代数における非常に重要な変換法則の一つです。これは、複数の項の否定と各項の否定とを関連づける法則です。具体的には、任意の変数 A と B に対して、次の2つの法則があります。

  • 論理和の否定:

変数AとBの論理和を否定すると、各変数を個別に否定してから論理積を取ったものと等しい、という関係を示しています。

    $$ \overline{A + B} = \overline{A} \cdot \overline{B} $$

ド・モルガンの法則はベン図を使うと簡単に証明できます。以下にベン図とMIL記号で示します。

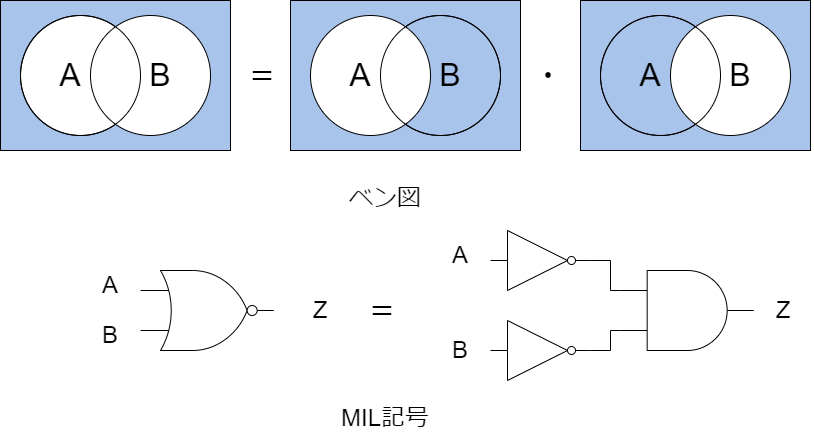
  • 論理積の否定:

変数AとBの論理積を否定すると、各変数を個別に否定してから論理和を取ったものと等しい、という関係を示しています。

    $$ \overline{A \cdot B} = \overline{A} + \overline{B} $$

以下にベン図とMIL記号で示します。

確認テスト

論理関数②確認テストはこちら

Follow me!

-デジタル回路, 回路, 論理関数, 高専2年生
-, , ,

PAGE TOP