前回の授業(【論理代数①】数の表現 )で紹介した2進数を人間に伝えるためには10進数へ変換する必要があります。時には2進数との変換が容易な8進数や16進数が用いられることがあり,今回の授業ではその変換について学んでゆきます。

表1 10進数とその他基数の比較
| 10進数 | 2進数 | 8進数 | 16進数 |
|---|---|---|---|
| 0 | 0000 | 0 | 0 |
| 1 | 0001 | 1 | 1 |
| 2 | 0010 | 2 | 2 |
| 3 | 0011 | 3 | 3 |
| 4 | 0100 | 4 | 4 |
| 5 | 0101 | 5 | 5 |
| 6 | 0110 | 6 | 6 |
| 7 | 0111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |


10進ー2進変換
10進数を2進数に変換する手順は以下のようになります。
- 除算のスタート: 10進数の値を2で除算します。この時の商と余りをメモします。
- 余りの記録: 最初の除算の余りが2進数の最下位(右端)の値となります。
- 商を使っての繰り返し: 前のステップの商を新しい数値として再び2で除算します。この新しい余りは2進数の次の位置の値となります。
- 終了条件: 商が0になるまでステップ2と3を繰り返します。
- 結果の読み取り: 全ての余りを逆順(最初の余りを最後に)に並べると、それが10進数を2進数に変換した結果となります。
例: 10進数の13を2進数に変換する場合の手順を詳しく見てみましょう。
- 13 ÷ 2 = 6...余り1
→ 最初の余りは1 - 6 ÷ 2 = 3...余り0
→ 2つ目の余りは0 - 3 ÷ 2 = 1...余り1
→ 3つ目の余りは1 - 1 ÷ 2 = 0...余り1
→ 4つ目の余りは1
上記の余りの値を逆順に並べると「1101」となります。したがって、10進数の13は2進数では「1101」となります。
筆算で示すと以下の通りです。

2進ー10進変換
2進数を10進数に変換する手順は以下の通りです。
- 各桁の確認: 2進数の各桁が表す数値を確認します。最右端(最下位)は
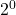 、その左は
、その左は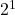 、さらにその左は
、さらにその左は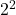 という風に、左へ進むごとに2のべき乗が1つ増えていきます。
という風に、左へ進むごとに2のべき乗が1つ増えていきます。 - 桁の値を乗算: 各桁の2進数の値(0または1)を、その桁が表す2のべき乗の数値と乗算します。
- 乗算結果の合計: ステップ2で得られた各乗算結果を合計すると、それが2進数を10進数に変換した結果となります。
例: 2進数の1101を10進数に変換する場合の手順を詳しく見てみましょう。
- 各桁の値を確認します。
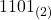
各桁のべき乗は以下のようになります。
- 各桁の値を乗算します。
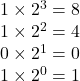
- すべての乗算結果を合計します。
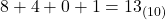
したがって、2進数の1101は10進数で13となります。
2進ー8進変換
2進数から8進数への変換は、基本的には2進数を3桁ずつグループ化して変換する方法を取ります。これは8進数の1桁が、2進数の3桁![]() で表現されるためです。
で表現されるためです。
以下に、2進数を8進数に変換する手順を詳しく説明します:
- 2進数を右から3桁ずつに区切る: 与えられた2進数を、右端から3桁ずつに区切ります。左端で桁数が足りない場合は、0で埋めます。
- 各グループを8進数に変換: それぞれの3桁の2進数グループを、対応する8進数の数値に変換します。以下は、3桁の2進数とそれに対応する8進数の関係です:
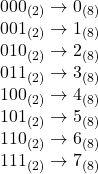
- 結果を並べる: ステップ2で得られた8進数の桁を、左から右へと並べることで、完全な8進数の数値が得られます。
例: 2進数![]() を8進数に変換する場合の手順を詳しく見てみましょう。
を8進数に変換する場合の手順を詳しく見てみましょう。
- 右から3桁ずつに区切ります。
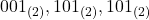
- 各グループを8進数に変換します。
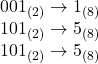
- 結果を並べます。
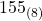
したがって、2進数の![]() は8進数で
は8進数で![]() となります。
となります。
また、その逆を行えば8進数を2進数に変換する事が可能です。このことから10進数よりも8進数の方が2進数との親和性が高い事が分かります。
2進ー16進変換
2進-8進の変換と同様,16進数も直接変換することが出来ます。基本的には2進数を4桁ずつグループ化して変換する方法を取ります。これは、![]() (16進数)が
(16進数)が![]() のため、16進数の1桁が2進数の4桁で表現されるからです。
のため、16進数の1桁が2進数の4桁で表現されるからです。
以下に、2進数を16進数に変換する手順を詳しく説明します:
- 2進数を右から4桁ずつに区切る: 与えられた2進数を、右端から4桁ずつに区切ります。左端で桁数が足りない場合は、0で埋めます。
- 各グループを16進数に変換: それぞれの4桁の2進数グループを、対応する16進数の数値や文字に変換します。
以下は、4桁の2進数とそれに対応する16進数の関係です:
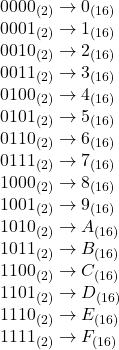
- 結果を並べる: ステップ2で得られた16進数の桁を、左から右へと並べることで、完全な16進数の数値が得られます。
例: 2進数 ![]() を16進数に変換する場合の手順を詳しく見てみましょう。
を16進数に変換する場合の手順を詳しく見てみましょう。
- 右から4桁ずつに区切ります。
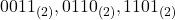
- 各グループを16進数に変換します。
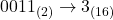
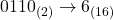
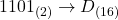
- 結果を並べます。
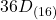
したがって、2進数の ![]() は16進数で
は16進数で ![]() となります。
となります。
