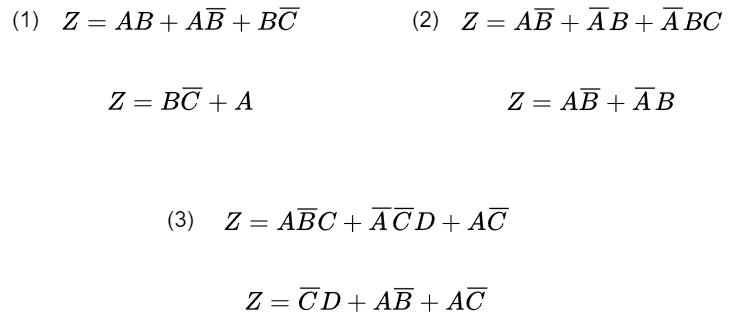今回はクワイン氏が提案し、マクラスキー氏が発展させたクワインーマクラスキー法について勉強していきます。この手法は簡単化の過程が機械的な為、プログラムのアルゴリズムとして実装しやすく、多くの変数を扱う論理関数の簡単化に適しています。

クワイン-マクラスキー法の手順
カルノー図による簡単化の方法は加法標準形の最小項を平面図で示しました。一方でクワイン-マクラスキー法(Q-M法)では最小項を表にして並べ、隣接する2つの最小項をすべて比較し、1変数ずつ機械的に消去していきます。簡単化の過程でこれ以上簡単化できない項の事を主項といいますが、Q-M法はこの主項を機械的に作り出す方法です。
例題として以下の論理関数をQ-M法を使って簡単化してみます。
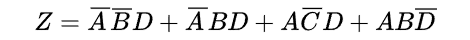
1.加法標準形を求めます。
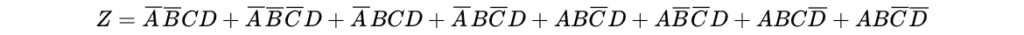
2.各最小項を1となる変数の個数毎にグループ分けし、個数の少ない順に並べた表を作ります。
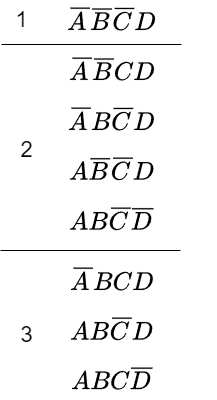
3.上下のグループ間ですべての項の組み合わせで比較を行い、1変数だけ異なる項(隣接項)を探します。またグループ1と2の比較と2と3の比較のグループに分けます。この際、組み合わせが見つかった項に✓マークを付けておきます。見つからなかった項はこれ以上は簡単化できない主項となります。
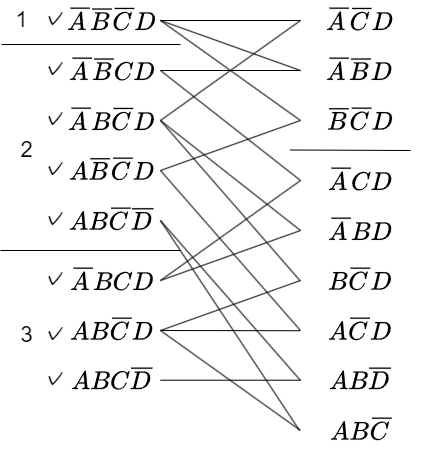
4.同様に2つのグループで比較を行い、隣接項を探します。組み合わせが見つかった項に✓マークを付けておきます。組み合わせを探す際に重複する項が出てきた場合は削除します。
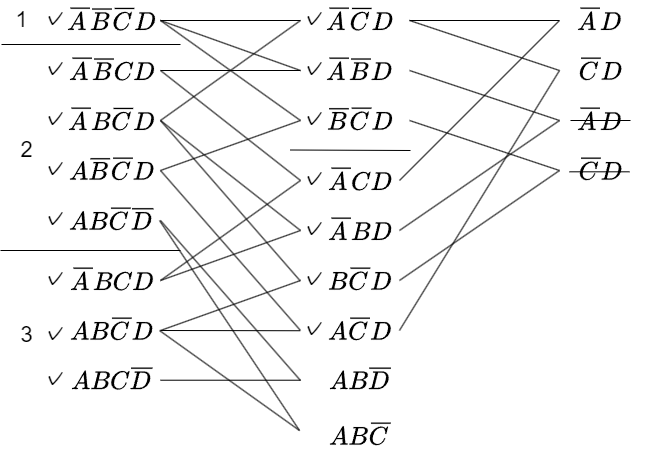
5.これ以上は簡単化できない為、下記の式が得られます。
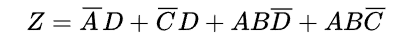
6.ここで、Q-M法は機械的にすべての項を比較して簡単化を行うため一度簡単化された高が再度簡単化されることがあります。そのため、最終的に得られた主項の中には重複する主項も出現する事があります。重複を消す為には以下のような最小項と主項の表を作成し、すべての最小項が含まれるかつ、重複しない主項を選択します。
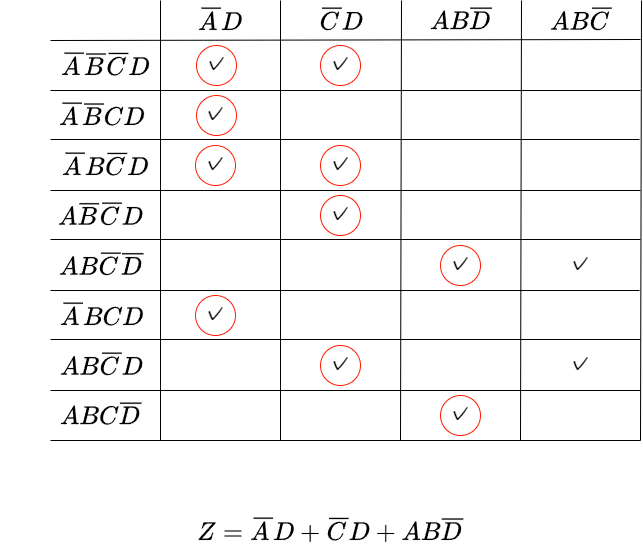
上の表を見ると、![]() は無くても、他の主項ですべての最小項が賄えている事が分かります。よって最終的に一番簡略化された式は上記のようになります。
は無くても、他の主項ですべての最小項が賄えている事が分かります。よって最終的に一番簡略化された式は上記のようになります。
練習問題
以下の論理関数をQ-M法を用いて簡単化せよ。
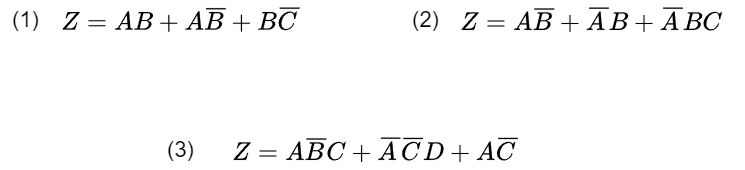
解答はこちらをクリック